Have you ever heard about nature’s most astonishing number?
Let me introduce a natural number sequence and a unique number that plays one of the main roles in the beauty of nature. I would like to say that you would find this number in a small seashell as well as in a giant spiral galaxy.
Starting from introducing the number sequence, The Fibonacci Sequence.
This name “Fibonacci sequence” was first used by a French mathematician Édouard Lucas.
The Fibonacci sequence is an infinite series of numbers starting with 1, and then again 1 then continue as the next number is the addition of the previous two numbers,.
1, 1, 2, 3, 5, 8, 13, 21, 34, 55…
The mathematical definition is:
X1 = X2 =1 and for each n > 2, Xn = Xn-1 + Xn-2 Where n is a natural number.
Why is it named as “Fibonacci”?
Leonardo Pisano Bogollo was an Italian mathematician and he lived between 1170 and 1250 in the Republic of Pisa. “Fibonacci” was his nickname, which roughly means “Son of Bonacci”.
Fibonacci’s problem on finding the growth of a population of rabbits with some assumptions was a biologically unrealistic scenario, where he used this sequence for the calculations and also it is the first time this sequence appears in a book (Liber Abaci (1202)).
Anyhow the history of The Fibonacci sequence is running to Indian mathematics from 1200 BC. Here, it’s worth saying something about Acharya Hemachandra who was an Indian Jain mathematician who lived between 1088 and 1173. He wanted to solve this question.
“How many rhythm patterns with a given total length can be formed from short and long syllables?”
He has described a number of sequences when presenting the solution to this question on rhythm patterns which was exactly the Fibonacci sequence. But this has happened around 1150, about fifty years before Fibonacci (1202). Because of this reason, some are naming the Fibonacci sequence as Hemachandra’s sequence. If you are interested in Hemachandra’s question on rhythm patterns, I recommend watching the below 12 mins YouTube video of Fields Medal winner, mathematician Manjul Bhargava’s explaining this.
Math class with Manjul Bhargava
Considering the digits “1, 1, 2, 3” of the sequence, November 23rd has marked as the Fibonacci Day. So next Nov 23 let everyone know!
That is enough to introduce the number sequence.
What if we make squares with those numbers in the sequence as widths and fit them side to side?
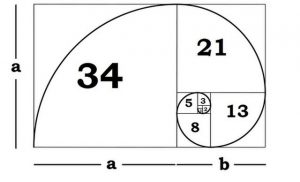
This visualization of the Fibonacci sequence is amazing. The number inside each of the squares illustrate the side length of the square. A spiral can be drawn inside the squares by connecting the corners of the boxes.
What do you know about The Golden Ratio?
The Golden ratio “φ” is an irrational real number that is the solution to the quadratic equation x2-x-1=0.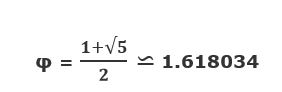
Using the definition of the golden ratio we can prove the above results. But I’m not going to do it here. The Fibonacci numbers are strongly related to the Golden ratio. The ratio of two consecutive Fibonacci Numbers is very close to the Golden Ratio.
In the above visualization, we can find the rectangles where the height is a Fibonacci number and the width is the sum of the consecutive Fibonacci numbers. (e.g.: a and a+b). These rectangles are also known as the Golden Rectangles because the ratio of the side lengths of these rectangles is close to the Golden Ratio.
When the Fibonacci sequence number gets larger, the ratio gets closer to the golden ratio.
So, now we know the simple number sequence and a unique number. But have we ever noticed these in the real world? Let’s discuss this.

What has attractiveness in a face got to do with mathematics? The answer is quite surprising. Regardless of skin color, age, gender or race a beautiful face is said to have many Golden ratios across including the ratio of the height and the width of the face. Not only the face, this proportion connected with the human body as well. So, more beauty with more golden ratios.

Many kinds of research have been conducted on the architectural models and have found that the golden ratio is present in many architectures including Pyramids in Egypt, Parthenon in Greece etc.
A famous painting, known as the Mona Lisa, painted by one of the greatest painters and a mathematician of all time, Leonardo Da Vinci, is drawn according to the golden ratio. Also, this is not his only painting drawn using the golden ratio.

Aston Martin gained some great press on its extensive application of the golden ratio in the design of the DB9.
It has observed that most of the world-famous artists, designers, architects and others have either intentionally or unintentionally used the golden ratio in their creations. We have caught this unique number hiding behind the beauty. So where is the number sequence we talked about earlier?
Did you know that the number of petals in any of the flowers is a Fibonacci number? Here are some examples.
- 1 Petal – Anthurium

- 2 Petals – Commelina
- 3 Petals – Lily
- 5 Petals – Wild rose
- 8 Petals – Delphinium
- 13 Petals – Cineraria
- 21 Petals – Aster
- 34 Petals – Plantain
See the seed head arrangement in the head of the sunflower. Not only in a sunflower, but lots of flowers also have a seed arranged in a spiral of Fibonacci numbers.
The spiral of Fibonacci numbers can be observed in most of the natural spirals ranging from Seashell to the spiral galaxy. Fibonacci sequences are indeed found everywhere in nature and the above examples that I have mentioned are only to give you an idea about the range that it has been expanded.


Finally, I would like to discuss the Contribution of the golden ratio and the Fibonacci number sequence for the IT industry. Here are some examples that I have found and there should be many more.
UI Development

According to experts, maintaining the golden ratio when designing the grid layouts of software or a web application will make an extra attraction of users on the application rather than using different colors and pictures. So it’s better to consider the ratio of the grids of your application to make it more attractive because the eye grasps it more quickly.
Data structure
Fibonacci heap is a data structure for priority queue operations with a better-amortized running time which beats many other priority queue data structures including both binary heap and binomial heap.
Search technique
Fibonacci search technique is a method of searching a sorted array using Fibonacci numbers. Compared to binary search both works for sorted arrays and has an average- and worst-case complexity of O (log n). But the Fibonacci search divides the array into two unequal parts that have sizes that are consecutive Fibonacci numbers. This has the advantage that division or multiplication, operations don’t use. When the input array is big and cannot fit in CPU cache/RAM, Fibonacci Search can be useful.
That is all I’m going to discuss on this Topic. If you are interested in Fibonacci Numbers, you can visit the below link to see more surprises.
The Mathematical Magic of the Fibonacci Numbers
References

